안녕하세요. 바로 이전 글인 테브난 정리, 노턴의 정리에 이어 오늘은, 중첩의 원리에 대해 간단하지만 자세하게 다뤄보도록 하겠습니다. 위 3가지 개념들은 대학 전공인 회로이론에서 배우는 내용인데요, 이는 전기기사의 회로이론 파트에도 자주 출제되는 개념들입니다. 다수의 전원이 있는 회로를 볼 때 유용하게 적용할 수 있는 중첩의 원리에 대해 함께 알아볼까요?

🔹 중첩의 원리(Superposition)란?
선형 시스템에서, 여러 개의 입력이 동시에 작용할 때 (하나의 회로에 다수의 전원이 존재할 때) 그 결과는 각 입력에 대한 개별 반응의 합과 같다는 원리입니다.
예를 들어,
만약 선형 시스템이고, 입력 A1이 결과 R1을 만들고, 입력 A2가 결과 R2를 만든다면
입력 A1 + A2 에 대한 시스템의 반응은 R = R1 + R2가 됩니다.
즉 전체 반응 = 부분 반응들의 합 이라고 볼 수 있습니다.
앞서서 중첩의 원리는 회로에 다수의 전원을 포함한 회로를 해석할 때 유용하다고 했는데요,
테브난의 정리, 노턴의 정리와 같이 전원 변환 및 단순화 방법을 통해서도 해석이 가능하지만,
만약 회로가 상당히 복잡하게 구성되어 있다면 위와 같은 정리를 적용하기에 어려움이 있을 것입니다.
이때 '중첩의 원리'를 이용한다면 전원이 여러 개 있는 회로라도 쉽게 해석할 수 있습니다.
🔹 전기회로에서의 중첩의 원리
전기회로에서는 복수의 독립 전압원 또는 전류원이 있을 때 각 독립 전원에 의한 전류 또는 전압을 개별적으로 계산한 다음, 그 값들을 더해서 전체 회로의 전류 또는 전압을 구할 수 있습니다.
여기서 매우 중요한 점은, 회로가 선형 (Linear) 이어야 합니다.
'선형'이라는 개념은 중첩의 원리나 회로 해석의 기본 전제가 되는 아주 중요한 개념입니다.
간단하게 말해서 선형이란, 입력과 출력 사이의 관계가 선형적인 시스템을 말합니다. 즉 다음 2가지 성질을 만족하는 회로를 선형 회로라고 합니다.
1. 동일성 (Homogeneity or Scaling): 입력을 x에서 ax로 바꾸면, 출력도 y에서 ay로 바뀌는 성질 (예, 입력 전압이 2배면 출력 전류도 2배)
2. 가법성 (Additivity): 두 개의 입력 x1, x2가 있을 때, 출력도 그 합이 되는 성질 (예, 입력이 x1 + x2 이면 출력은 y1 + y2)
※ 저항, 인덕터, 커패시터 등은 선형 소자 / 다이오드, 트랜지스터는 비선형 소자로 분류됩니다.
또한 중첩의 원리는 회로 내에 독립 전원이 두 개 이상 존재했을 때 쓸모가 있습니다.

위 사진은 회로의 동등성과 선형성을 알려주는 표 사진이며, 아까 말했듯이 선형성은 Homogeneity와 Additivity 를 모두 만족해야 합니다. 주의할 점은 방향이나 크기가 다른 전류원을 직렬로 연결하거나, 전압원을 병렬로 연결하는 것은 안됩니다. 위 형태는 기본으로 알아두시면 좋을 것 같아 함께 첨부합니다.
그럼 중첩의 원리는 어떻게 적용하는 걸까요?
STEP 1. 하나의 독립 전원만 활성화시키고, 나머지 전원은 모두 제거합니다.
- 전압원은 단락 (short) → 0V
- 전류원은 개방 (open) → 0A
STEP 2. 활성화시킨 해당 전원 하나만 있는 상태에서 회로를 해석합니다. (전류 또는 전압 구하기)
STEP 3. 모든 독립 전원에 대해 위 과정을 반복합니다.
STEP 4. 각 전원에 의한 전압 / 전류의 결과를 합산하여 전체 회로의 해석 결과를 얻으면 됩니다.
예제를 통해 위 과정을 다시 한번 풀어서 설명해보겠습니다.
아래와 같은 회로가 있다고 합시다.
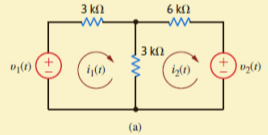
먼저, 위 (a) 회로의 i1(t)를 구하기 위해서 v1(t) 전원만 놔두고, 나머지 전원 v2(t)는 제거해줍니다. 그럼 아래 그림의 (b)와 같은 회로가 되고, 이 회로에서 i'1(t)를 구해주면 됩니다.
반대로 i2(t)를 구하려면 v2(t) 전원은 놔두고, 왼쪽의 v1(t)를 없애주면 되겠죠? 전압원이니까 단락(short) 시켜줍니다. 그럼 아래 그림의 (c)와 같은 회로가 되고, 이 회로에서 i'2(t)를 구해주면 됩니다.

여기서 끝내면 절대 안됩니다 !!!
주어진 실제 회로는 (a) 회로이고, 구해야 하는 건 (a) 회로의 i1(t)과 i2(t) 입니다.
따라서 (b), (c) 회로에서 구한 각각의 i'1(t)와 i'2(t)를 더해줌으로써 (a) 회로의 각 저항에 흐르는 전류를 구할 수 있습니다.
참고로 전류, 전압을 계산하실 때는 키르히호프 법칙 KCL, KVL 등을 이용해서 구하시면 됩니다.
위 회로 그림은 개념 이해를 도우기 위한 예제였습니다.
다음 회로를 통해 중첩의 원리 적용 및 실제 저항 6옴에 흐르는 전류를 계산해보겠습니다.

위와 같은 회로가 있다고 합시다. 독립 전원이 2개가 있고, 하나는 전압원, 하나는 전류원인 회로입니다.
아래 과정으로 중첩의 원리를 적용해보겠습니다.
※ 이해하고 넘어가기
1. 하나의 독립 전원만 활성화시키고, 나머지 전원은 모두 제거합니다.
2. 활성화시킨 해당 전원 하나만 있는 상태에서 회로를 해석합니다. (전류 또는 전압 구하기)
3. 모든 독립 전원에 대해 위 과정을 반복합니다.
4. 각 전원에 의한 전압 / 전류의 결과를 합산하여 전체 회로의 해석 결과를 얻으면 됩니다.
STEP 1. 전압원 그대로, 전류원 개방

그리고 출력 단자 a, b를 지정해주고, 이 단자에서 회로를 바라본 상태에서 등가저항 및 6옴에 흐르는 전류를 계산해보겠습니다. 계산 과정은 다음과 같습니다.
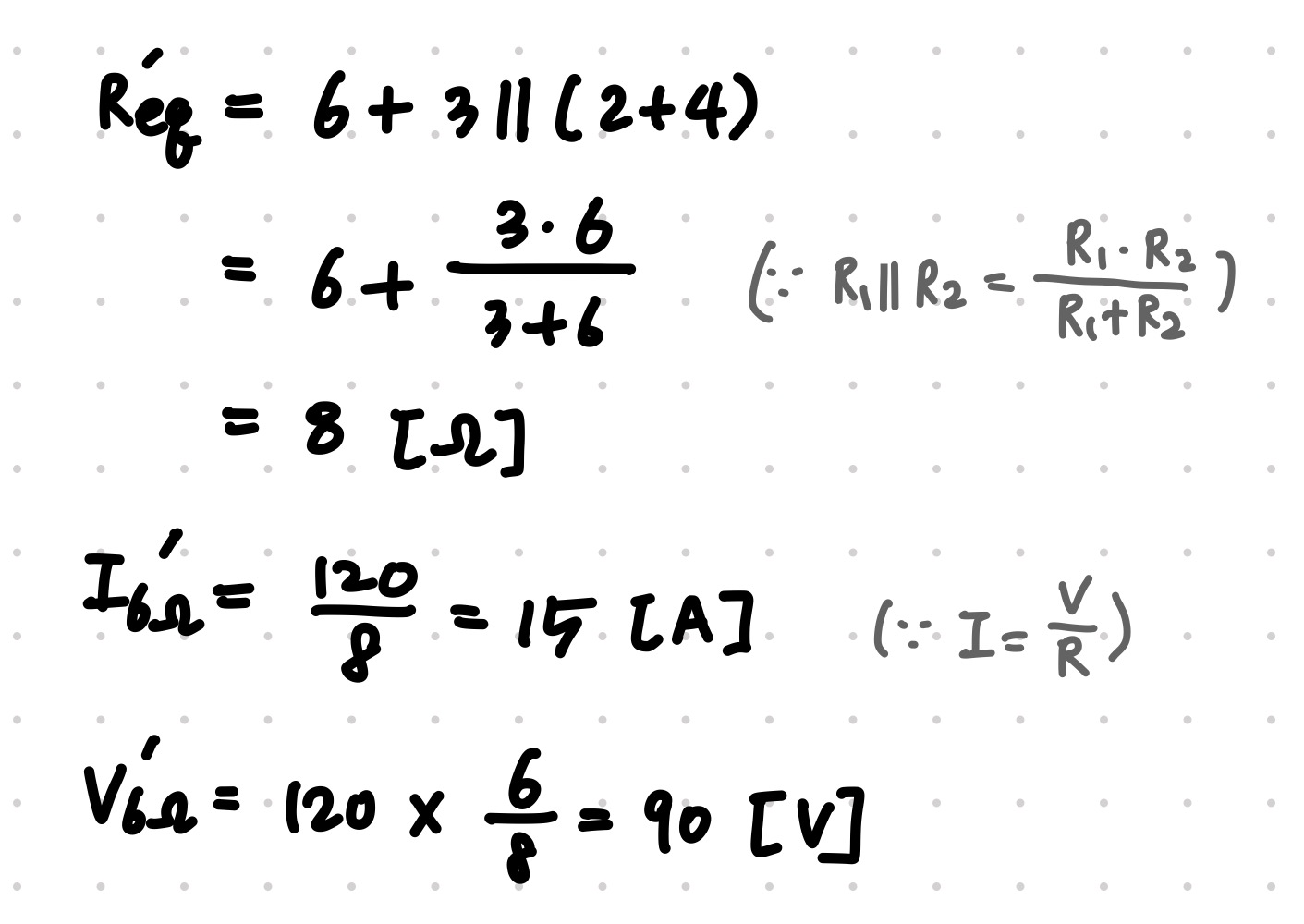
a, b 단자에서 바라보면 저항 2옴과 4옴은 직렬이고, 이것들과 3옴이 병렬연결, 그리고 나머지 6옴과 직렬연결인 상태입니다. 그래서 계산해주면 R'eq = 8 옴입니다.
옴의 법칙을 통해서 저항 6옴에 흐르는 전류는 120/8 = 15 A 임을 알 수 있습니다.
추가로 전압 분배 법칙을 사용하여 전체 저항 중 6옴에 걸리는 전압을 계산해보면 120 x (6/8) = 90V 가 됩니다.
STEP 2. 전류원 그대로, 전압원 단락

전류원 바로 옆에 병렬 연결되어 있는 4옴은 놔두고, 왼쪽의 3개의 저항을 계산해주겠습니다.

저항 6옴과 3옴은 병렬연결, 그리고 이것들과 2옴이 직렬연결된 상태입니다. 따라서 계산해주면 노란 박스의 저항 R''eq = 4 옴이 나옵니다.
자 그럼 위에서 구해준 4옴과 전류원과 병렬연결된 4옴 두 개가 남아있죠? 이걸 바탕으로 전류원 바로 옆에 있는 4옴에 걸리는 전류의 크기를 계산해주겠습니다.
4 || 4 = 2 옴이고, 여기에 걸리는 전압 V = I R = 12 x 2 = 24V, 저항 4옴에 흐르는 전류의 크기는 I = V / R = 24 / 4 = 6A 입니다. (방향을 고려하여 부호와 같이 표시하면 -6A)

Node를 기준으로 KCL (키르히호프 전류 법칙)을 적용하면 R''eq에 흐르는 전류는 -6A가 되고, 전류 분배 법칙을 통해 저항 6옴에 흐르는 전류를 계산해주면 -2A가 나옵니다.
최종적으로 저항 6옴에 걸리는 총 전류는 위에서 구한 I' 과 I''를 더해주면 됩니다.
여기서 주의할 점 !!!!!
전류의 방향을 꼭 고려해서 회로를 해석해야 합니다. 전류의 방향을 먼저 정하고, 회로를 해석해주면 됩니다.


따라서 저항 6옴에 흐르는 전류는 17옴으로 계산되었습니다.
이렇게 해서 중첩의 원리의 개념에 대해 먼저 알아보고, 예제 및 회로에 직접 적용해봄으로써 저항에 흐르는 전류값을 구해보았습니다. 실제로 실험이나 회로 문제를 풀어보면 테브난, 노턴 등가회로에 이어 중첩의 원리도 정말 중요하구나를 느낄 수 있을 것입니다. 시험에서도 자주 나오고, 현재 전기기사 회로이론 파트에도 자주 출제되는 이론들이니 꼭 이해하고 넘어가셨으면 좋겠습니다. 학습에 도움 되셨길 바라며, 시험을 준비하고 있다면 좋은 결과 있으시길 바라겠습니다.
'Engineering > 회로' 카테고리의 다른 글
| 전기기사 수변전 설비 결선도에 쓰이는 약호, 명칭, 용도(역할) 간단 정리 (0) | 2025.05.21 |
|---|---|
| 테브난의 정리, 노턴의 정리란? (0) | 2025.04.29 |
| 전기기사 논리식, 논리등가회로, 드모르간의 법칙, 불 대수 (0) | 2025.04.21 |
| 진상 전류, 지상 전류란? 개념, 공식, 활용, 둘의 관계 (0) | 2025.03.28 |
| 인덕터, 상호 인덕턴스란? 개념, 공식, 유도 전압 (0) | 2025.03.28 |



