전기기사 회로이론 부분에서 출제되는 인덕터와 상호 인덕턴스, 그리고 이와 관련된 공식에 대해서 다뤄보겠습니다. 관련 문제들도 있으니 문제 풀이해보고 답을 맞춰보시길 바랍니다. 틀린 문제에 대해서는 개념과 공식을 다시 익히신 후, 오답 풀이를 하시는 걸 추천 드립니다. 그럼 인덕터에 대해서 알아볼까요?
1. 인덕터의 전압-전류 관계
인덕터의 전압과 전류는 다음의 기본적인 미분 방정식으로 표현됩니다.

여기서,
- vL : 인덕터 양단의 전압 (단위: V)
- L : 인덕턴스 (단위: H, Henry)
- d : 인덕터를 흐르는 전류의 시간에 대한 변화율
이 식은 전류의 변화량이 있을 때만 인덕터에 전압이 형성된다는 것을 의미합니다. 즉, 전류가 일정하면 인덕터의 전압은 0V가 됩니다.
2. 전류 방향과 전압 극성
(1) 패시브 부호 규칙 (Passive Sign Convention)
- 인덕터에 전류가 흐르는 방향으로 보면 전류가 들어가는 단자가 (+), 나오는 단자가 (-)가 됩니다.
- 즉, 전류가 증가할 때 인덕터 양단에 발생하는 전압은 전류 방향과 일치하는 단자가 높은 전압을 갖습니다.
- 전압과 전류의 방향이 아래와 같다면:
- 전류가 위에서 아래로 흐를 때
- 전압의 (+)극이 위쪽, (-)극이 아래쪽

(2) 능동 부호 규칙 (Active Sign Convention)
- 만약 외부 전원이 인덕터에 전압을 걸어 전류를 증가시키려고 하면, 인덕터의 전압은 반대 방향이 됩니다.
- 즉, 전압이 인가되었을 때 인덕터가 이에 대해 반발하는 성질(렌츠의 법칙) 때문에 외부에서 인가된 전압 방향과 반대 방향으로 유도 기전력이 형성됩니다.
- 전압 방향을 반대로 가정하면:
- 전류가 위에서 아래로 흐르는데, 위쪽을 (-), 아래쪽을 (+)로 하면

3. 요약
- 패시브 부호 규칙 적용: 전류가 (+)단자로 들어가면

전압과 전류의 방향이 같을 때 - 능동 부호 규칙 적용: 전압이 외부에서 가해진다면

전압과 전류의 방향이 다를 때
즉, 인덕터에서 전류의 방향과 전압의 극성을 고려할 때 전류 방향이 설정된 기준에 따라 전압의 부호가 바뀌는 것을 이해하면 됩니다.
다음으로 상호 인덕턴스에 대해 알아볼까요?
상호 인덕턴스(Mutual Inductance)란?
상호 인덕턴스는 두 개의 코일(인덕터) 사이에 자기장이 결합하면서 한 코일의 전류 변화가 다른 코일에 영향을 주는 현상을 의미합니다. 이는 변압기, 모터, 발전기 등에서 중요한 개념입니다.
두 개의 인덕터가 자기적으로 결합되어 있을 때, 한 인덕터의 전류 변화가 다른 인덕터에 유도 전압을 발생시키는 관계를 수식으로 표현할 수 있습니다.
1. 기본 상호 인덕턴스 공식
두 개의 코일 L1, L2 사이의 상호 인덕턴스 M은 다음과 같이 정의됩니다.
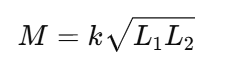
여기서,
- M : 상호 인덕턴스 (H, Henry)
- L1, L2: 각 코일의 자기 인덕턴스 (H)
- k : 결합 계수 (0 ≤ k ≤ 1, 자기적 결합의 강도를 나타냄)
결합 계수 k는
- k=1 : 완전 결합 (모든 자기장이 상대 코일에 영향을 줌)
- k=0: 결합 없음 (각 코일이 독립적으로 동작)
- 일반적으로 k는 0~1 사이의 값을 가짐
2. 상호 유도 전압 공식
패러데이의 법칙에 의해 상호 인덕턴스가 있는 경우, 한 코일의 전류 변화가 다른 코일에 유도 전압을 생성합니다.
(1) 코일 1의 전류 변화가 코일 2에 유도 전압을 생성할 때

- v2 : 코일 2에 유도된 전압
- M : 상호 인덕턴스
- di1/dt : 코일 1의 전류 변화율
(2) 코일 2의 전류 변화가 코일 1에 유도 전압을 생성할 때

- v : 코일 1에 유도된 전압
- di2/dt : 코일 2의 전류 변화율
이 식은 변압기와 같은 장치에서 1차 코일의 전류 변화가 2차 코일에 영향을 주는 원리를 설명합니다.
3. 결합된 인덕터의 등가 인덕턴스
(1) 직렬 연결 (Mutually Coupled Inductors in Series)
- 두 인덕터가 같은 방향으로 권선되었다면:


- 두 인덕터가 반대 방향으로 권선되었다면:
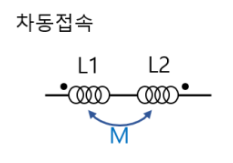

(2) 병렬 연결 (Mutually Coupled Inductors in Parallel)
- 같은 방향일 경우:

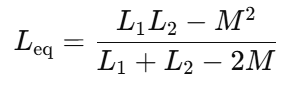
- 반대 방향일 경우:


병렬 인덕턴스 공식
이 공식들은 두 개의 인덕터를 병렬 또는 직렬로 연결할 때 회로의 등가 인덕턴스를 구하는 데 사용됩니다.
4. 상호 인덕턴스의 활용 예시
- 변압기: 1차 코일과 2차 코일 사이의 자기 결합을 이용해 전압을 변환.
- 무선 충전 시스템: 자기장을 통해 에너지를 전송하는 원리.
- 모터 및 발전기: 회전하는 자기장을 이용해 전력을 생산하거나 소비.
정리
✅ 상호 인덕턴스 공식
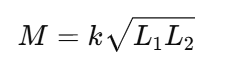
✅ 유도 전압 공식

✅ 등가 인덕턴스 (직렬 및 병렬 연결 시)
이 개념들은 전기기사 회로이론뿐만 아니라 전력 시스템, 통신 시스템 등에서도 중요한 역할을 합니다.
상호 인덕턴스 관련 문제 3개
문제 1: 상호 인덕턴스 계산
서로 결합된 두 개의 코일이 있으며, 각 코일의 자기 인덕턴스는 다음과 같습니다. L1 = 4H, L2 = 9H, 결합 계수 k=0.6일 때 상호 인덕턴스 M을 구하시오.
문제 2: 유도 전압 계산
두 개의 코일이 서로 결합되어 있으며, 상호 인덕턴스 M=2H 입니다. 코일 1에 흐르는 전류가 다음과 같이 변화할 때, 코일 2에 유도되는 전압을 구하시오.

문제 3: 등가 인덕턴스 계산 (직렬 결합)
서로 결합된 두 개의 인덕터 L1=5H, L2=3H, M=1.5H가 있습니다. 두 인덕터가 같은 방향으로 결합되어 직렬로 연결되었을 때, 회로의 등가 인덕턴스 Leq를 구하시오.
문제 정답
문제 1:

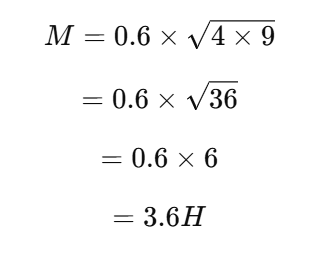
문제 2:
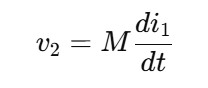


문제 3:


인덕터와 상호 인덕턴스의 개념, 그리고 인덕터가 직렬, 병렬로 연결되어 있을 때의 공식에 대해서 자세히 알아보았습니다! 전기기사 회로 이론만이 아닌 전력 시스템, 통신에서도 중요하게 다루는 상호 인덕턴스에 대한 문제들을 풀어보면서 상호 인덕턴스 개념을 확실히 이해하는 데 도움이 됐길 바랍니다😊
'전기기사' 카테고리의 다른 글
| 진상 전류, 지상 전류란? 개념, 공식, 활용, 둘의 관계 (0) | 2025.03.28 |
|---|---|
| 임피던스와 어드미턴스란? 개념, 공식, 관계, 예제 문제 (0) | 2025.03.28 |
| 전기기사 발전소 설비 관련 공식 모음 (0) | 2025.03.28 |
| 전선 종류? 전기기사에 나오는 전선 종류 비교 정리 (0) | 2025.03.20 |
| 코로나 방전이란? 발생 원리, 특징, 섬락과 차이점 (0) | 2025.03.19 |



