

안녕하세요. 오늘은 전기기사 회로이론 부분인 테브난 정리와 노턴 정리에 대해 자세히 다뤄보려고 합니다. 개인적으로 필기 기출 문제 풀이를 하며 느낀 것은 테브난, 노턴 정리 보다는 중첩의 원리를 이용한 문제들이 많았습니다. 그러나 테브난, 노턴의 정리와 관련된 문제들도 자주 출제되므로 위 개념 모두 잘 이해하는 것이 중요하다는 생각이 듭니다. 그럼 함께 알아볼까요? 참고로 제가 작성하는 모든 글은 제가 이해한 것을 바탕으로 작성한 글입니다.
테브난 정리와 노턴 정리에 대해 알아보기 전에,
왜 이러한 정리를 사용하는가? 에 대해서 간단히 다뤄보겠습니다.
테브난의 정리와 노턴의 정리를 잘 이해하고 응용한다면, 그 어떤 복잡한 회로도 간단한 등가회로로 만들어버릴 수 있습니다.
여기서 등가회로란?
실제 회로의 구성이 너무 복잡하면 이를 해석하는 데 시간이 많이 소요되고, 해석하기도 어렵습니다.
이때 회로의 전기적 특성은 유지하고, 복잡했던 회로요소들을 가장 단순한 형태로 조합하여 해석을 쉽게 할 수 있도록 구성한 회로를 등가회로라고 합니다.
저희도 복잡한 것보다는 단순한 걸 좋아하지 않습니까?
따라서 복잡한 것을 단순한 회로 형태인 등가회로를 구성하기 위해서는 테브난의 정리와 노턴의 정리를 이해하고 적용할 줄 알아야 합니다.
회로를 다루는 사람이라면, 테브난 정리와 노턴의 정리는 회로 구성 및 해석에 정말 중요한 정리라고 볼 수 있을 것 같습니다.
✅ 1. 테브난의 정리 (Thévenin's Theorem)
테브난 정리는 복잡한 회로를 하나의 전압원(V)과 직렬 저항(R)으로 바꿔주는 정리입니다.
어떤 2단자 회로도 전압원(Vth)과 직렬저항(Rth)으로 표현이 가능합니다.
외부에서 볼 때, 회로는 이 등가 회로와 동일하게 동작합니다. 즉, 전압원과 직렬저항으로 바꿔주어도 회로의 전기적 특성은 동일하다고 볼 수 있습니다.
테브난 정리로 회로 구성을 어떻게 바꾸는 건데?
1. 회로의 출력 단자를 개방(open)한 상태에서 전압을 측정합니다. → Vth (테브난 전압)
2. 전압원은 단락(short), 전류원은 개방(open)하여 저항만 남긴 회로에서 저항을 계산합니다. → Rth (테브난 저항)
예, 말로만 되어 있으니 뭐라고 하는지 잘 이해가 안 되실 겁니다. 아래 회로 그림과 같이 설명해보겠습니다.

왼쪽의 푸른 box에 실제 회로의 요소들이 복잡하게 구성되어 있다고 가정하겠습니다.
테브난의 정리는 전압원 1개와 저항 1개를 직렬 연결하여 간단한 회로로 변환해주는 정리라고 보시면 됩니다.
바로 위에서 1. 회로의 출력 단자를 개방한 상태에서 전압을 측정해야 한다고 했습니다. (테브난 전압)
회로 사진을 보면, 회로의 출력 단자는 a와 b이며, a와 b 단자 사이의 전압을 측정하는 것이 테브난 전압 Vth을 구하는 방법입니다.
등가회로로 바꾼다는 것은, 외부에 연결된 부하(load)입장에서 봤을 때 회로의 동작을 같게 만들겠다는 뜻입니다. 따라서 회로의 나머지 복잡한 부분을 a-b 단자 기준으로 단순화해서, 외부에 어떤 부하를 연결해도 동작이 같도록 만들어주는 것입니다.
다음 예제를 통해 [테브난의 정리] 전압원 Vth와 테브난 저항 Rth를 구해보겠습니다.
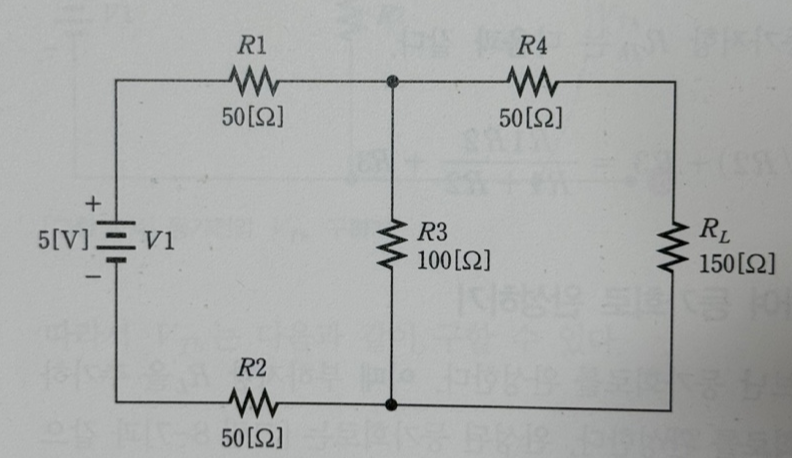
위 회로를 저희가 테브난 정리를 적용하기 전의 실제 회로라고 합시다.
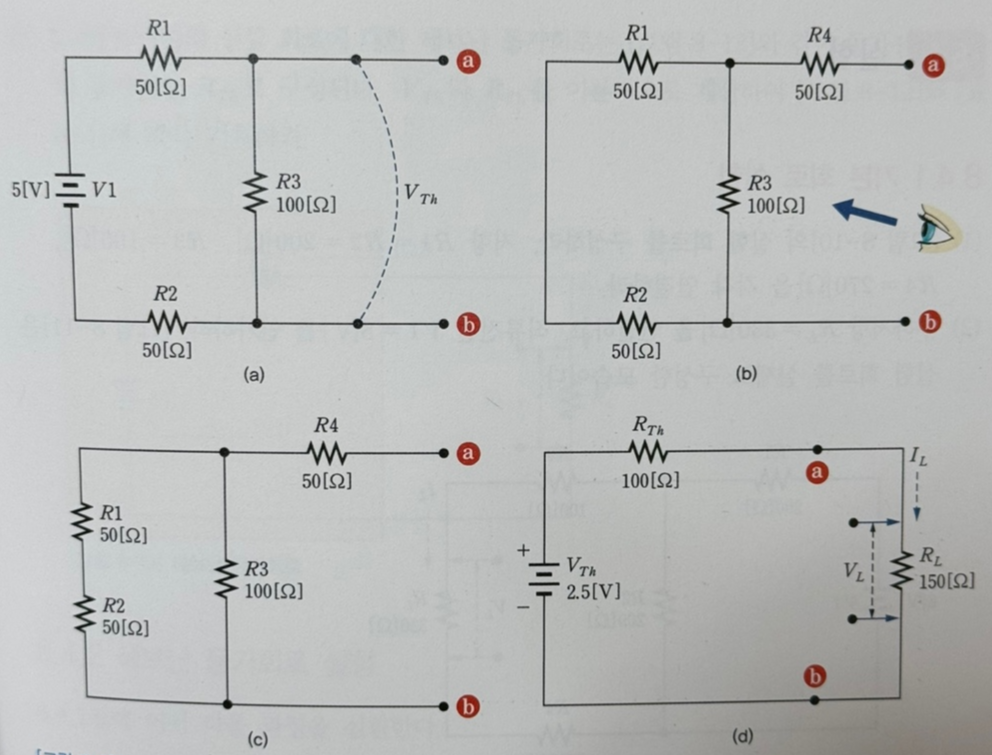
위 사진은 테브난 등가회로를 구하는 과정을 차례로 나타낸 그림입니다. (a) ~(b)
※참고)
1. 회로의 출력 단자를 개방(open)한 상태에서 전압을 측정합니다. → Vth (테브난 전압)
2. 전압원은 단락(short), 전류원은 개방(open)하여 저항만 남긴 회로에서 저항을 계산합니다. → Rth (테브난 저항)
먼저 실제 회로의 오른쪽 저항 RL의 위치에 단자 a, b를 설정하고, 단자 간을 개방합니다. 이로 인해 R4가 회로에서 제거 되었습니다.
이때 등가전압 즉, 테브난 전압 Vth는 저항 R3에 걸린 전압이므로 다음과 같이 구할 수 있습니다.

다음으로 등가저항 Rth를 구해보겠습니다.
앞서 설명했던 것과 같이 테브난 저항을 구하기 위해서 전압원은 단락, 전류원은 개방한 상태에서 구해야 합니다.
따라서 Rth는 그림 (b)와 같이 V1을 단락시킨 다음, 출력 단자 a, b에서 바라본 저항입니다.
회로를 단자 쪽에서 바라보면, R1과 R2가 직렬로 연결되고, 이것들과 R3가 병렬로 연결됩니다. R4는 R1~R3과 직렬로 연결됩니다. 이를 회로로 나타내면 그림 (c)와 같습니다. 따라서 Rth를 구하면 다음과 같습니다.
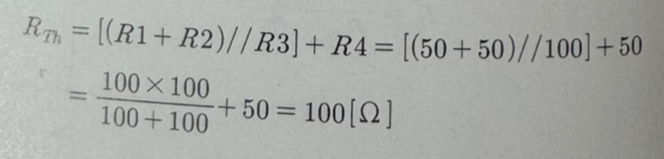
최종적으로 구한 Vth와 Rth를 이용하여 테브난 등가회로를 그리면 그림 (d)와 같습니다. (Vth, Rth 직렬 연결)
저항 RL의 전류 IL과 전압 VL을 구하는 문제였다면, 다음과 같이 구할 수 있습니다.
직렬 회로이며, 옴의 법칙을 이용하여 쉽게 구할 수 있습니다.
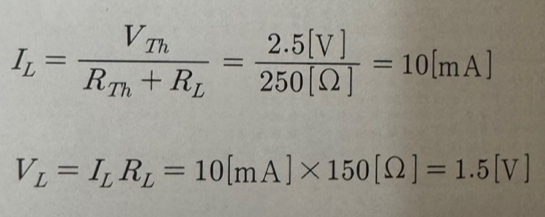
✅ 2. 노턴의 정리 (Norton's Theorem)
노턴의 정리는 복잡한 회로를 하나의 전류원(I)과 병렬 저항(R)으로 바꿔주는 정리입니다.
어떤 2단자 회로도 전류원 In과 병렬저항 Rn으로 표현이 가능합니다.
테브난 정리와 쌍을 이룹니다. (Rth = Rn, In = Vth/Rth 옴의 법칙 이용)
노턴 정리로 어떻게 바꾸는 건데?
1. 회로의 출력 단자에 단락을 연결하고 흐르는 전류를 측정합니다. → In (노턴 전류)
2. 전압원은 단락(short), 전류원은 개방(open)하여 저항만 남긴 회로에서 저항을 계산합니다. → Rn(노턴 저항)
저항 계산은 테브난과 동일합니다.

다시 말해서, 노턴의 정리는 부하를 제외한 전체 회로를 독립 전류원 하나와 저항 하나를 병렬 연결하여 간단한 회로로 변환해주는 정리라고 보시면 됩니다.
테브난 등가회로와 같이 a-b 단자에서 바라본 관점에서, 즉 외부에 연결된 부하 입장에서 노턴 전류와 노턴 저항을 계산해주어야 합니다.
다음 예제를 통해 [노턴의 정리] 전류원 In, 노턴 저항 Rn을 구해보겠습니다.
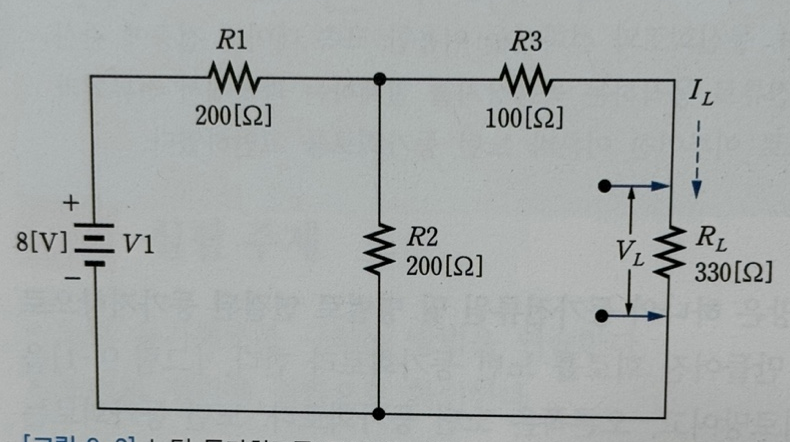
위 회로를 노턴의 정리를 적용하기 전의 실제 회로라고 합시다.
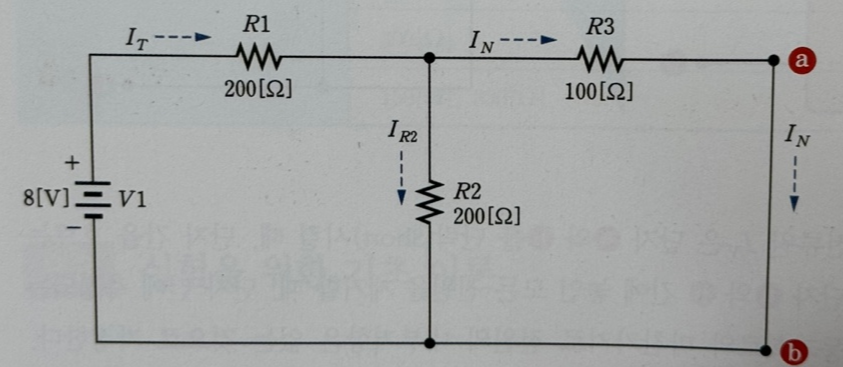
실제 회로의 부하저항 RL을 제거하고, 그 양 끝을 단자 a, b로 지정합니다.
노턴의 정리는 하나의 전류원과 하나의 병렬 저항을 이용한다고 말씀드렸죠?
등가 전류원을 구하기 위해 위 사진처럼 a, b 두 단자 간을 단락시킵니다.
부하저항 RL이 제거되고, a, b 단자 사이를 단락시키면 저항 R2, R3은 병렬 연결이 됩니다. 그리고 이것들과 R1이 직렬 연결됩니다. 따라서 전체 저항(R total)은 다음과 같이 계산됩니다.

전체 전류 (I total)은 옴의 법칙에 따라 다음과 같이 계산됩니다.

(노턴) 등가 전류원 In은 R3을 흐르는 전류와 같고 다음과 같이 계산됩니다.

등가회로를 구하는 첫 번째 단계였던 등가 전류원을 구했으니, 남은 단계는 등가저항 Rn 구하기 입니다.
등가 저항을 구하기 위해서 전압원은 단락시켜주고, 단자 a, b를 지정해주고, 단자 a, b 족에서 바라보면
R1과 R2는 병렬, 그리고 이들과 R3가 직렬로 연결되고 있습니다.
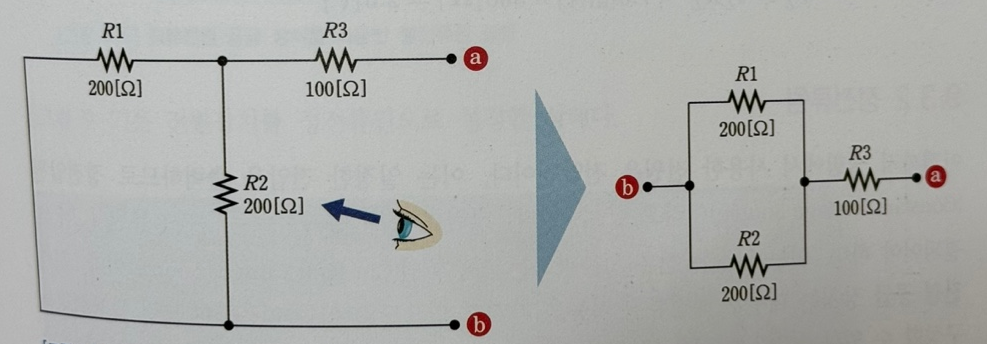
따라서 등가저항 Rn은 다음과 같이 계산할 수 있습니다.

최종으로, 앞에서 구한 등가전류원 In과 등가저항 Rn을 병렬로 연걸하면 노턴 등가회로가 됩니다.
이때, 처음에 저희가 맘대로 부하저항 RL을 제거했기 때문에 노턴 등가회로로 다시 구성할 때는 부하저항 RL을 추가해주어야 합니다.

노란색 박스 부분이 노턴 등가회로입니다.
문제에서 부하저항 RL의 전류 IL과 전압 VL을 구하라고 했다면, 다음과 같이 쉽게 구할 수 있습니다.

이렇게 기초회로실험, 회로이론, 전자회로, 전기기사에 중요한 테브난의 정리와 노턴의 정리에 대해 기초부터 간단하게? 자세히 다뤄보았습니다. 위 정리를 사용하는 이유, 등가회로의 장점부터 등가 전압원, 등가 전류원, 등가 저항을 직접 구해보면서 저도 테브난, 노턴의 정리 개념들을 다시 정리해볼 수 있었습니다. 학습 또는 자격증 준비에 도움이 되셨길 바라며, 좋은 결과 있으시길 바랍니다. 다음 글은 '중첩의 원리'에 대해 작성해보겠습니다.
'전기기사' 카테고리의 다른 글
| 전기기사 직류 전동기 속도 특성 곡선이란? (0) | 2025.05.07 |
|---|---|
| 중첩의 원리란? 적용 방법, 다수 전원이 포함된 회로 (0) | 2025.05.02 |
| 전동기, 발전기의 무부하 상태? 전부하 상태? 위상특성곡선 (0) | 2025.04.25 |
| 동기 전동기 위상특성곡선(V곡선)이란? 동기 전동기 작동 원리, 기동 방법 (0) | 2025.04.22 |
| 전기기사 논리식, 논리등가회로, 드모르간의 법칙, 불 대수 (0) | 2025.04.21 |



